Viral X post sparks debate over simple arithmetic; correct answer hinges on order of operations
A single-line equation posted to X divided users; mathematics conventions on multiplication, division and left-to-right evaluation determine the result
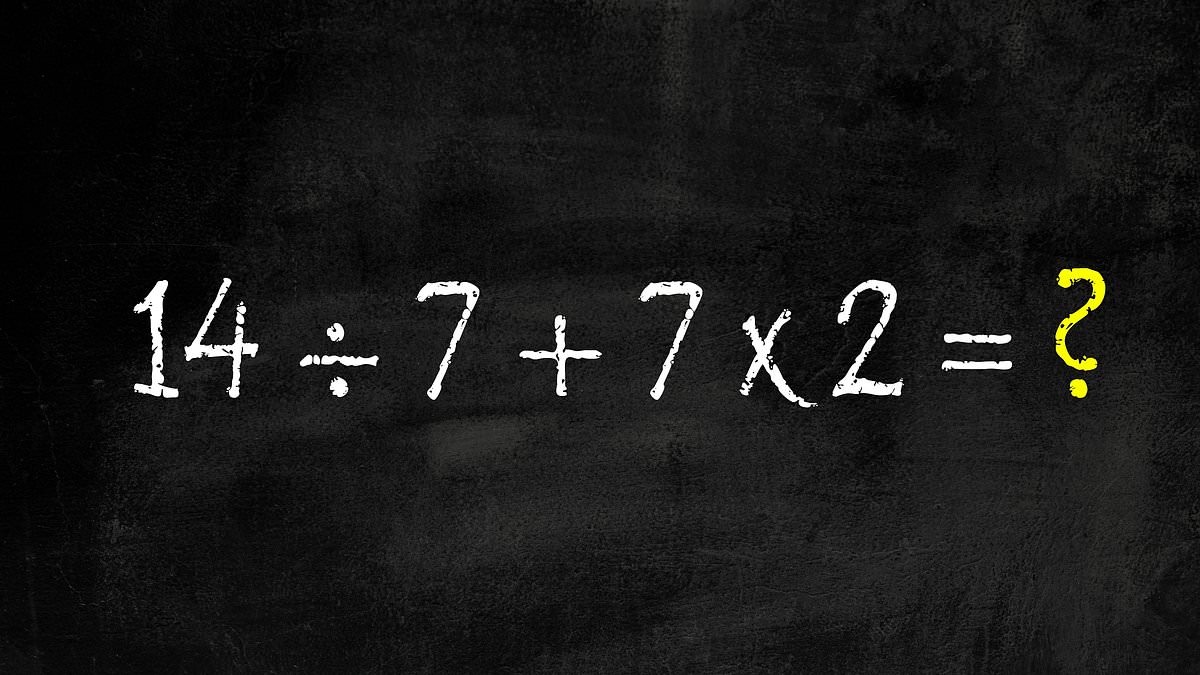
A short arithmetic problem posted to X by user @BholanathDutta this month prompted a wide online debate over the correct answer, highlighting common misunderstandings about the order of operations taught in basic mathematics.
The equation, written as 14 ÷ 7 + 7 × 2, produced a variety of answers in the post's comments, with responses ranging from single digits to numbers above 80. The correct solution, under standard mathematical conventions, is 16.
Mathematics educators and reference guides say the expression should be evaluated using the established order of operations. A common mnemonic in English is PEMDAS — Parentheses, Exponents, Multiplication and Division, Addition and Subtraction — but important nuance lies in the fact that multiplication and division share the same level of precedence and are carried out left to right. The same left-to-right rule applies to addition and subtraction.
Applying that rule to the viral problem, the leftmost operation is division: 14 ÷ 7 equals 2. Next, the multiplication 7 × 2 equals 14. With those intermediate results, the expression reduces to 2 + 14, which evaluates to 16. Doing the operations in a different sequence, such as performing addition before multiplication, produces an incorrect result.
The debate echoed familiar online patterns in which short, apparently simple problems expose gaps in recall about formal rules from school mathematics. Commenters invoked different mnemonics and intuitions: some treated multiplication as always preceding division, others evaluated strictly left to right, and a portion mistakenly applied a purely left-to-right reading to all operations, yielding various incorrect totals, including 18.
Mathematics curricula in many countries teach equal precedence for paired operations. For example, commonly used classroom guidance advises students that multiplication does not universally outrank division; instead, both are evaluated in the order they appear when scanning an expression from left to right. Teachers and reference texts offer worked examples to reinforce this point precisely because everyday reading habits can lead to misapplication.
The X thread and subsequent coverage amplified not only the specific arithmetic question but also renewed attention to how order-of-operations rules are presented and remembered. Experts who responded to similar viral puzzles recommend using parentheses to make intended grouping explicit when writing expressions, and encourage reworking problems step by step to verify intermediate values.
The post and the conversation that followed demonstrate how short, portable problems can function as informal tests of shared mathematical conventions. While calculators and digital tools perform these rules automatically, the dispute online served as a reminder that a clear understanding of equal precedence and left-to-right evaluation remains useful for checking work and communicating mathematical intent without ambiguity.